Feature Article

Air To Air Gunnery - Theory and Application, Part One

by Andy Bush

Introduction

I’ll never forget a piece of F-4 gun film from Vietnam. The F-4 pilot has gotten himself nicely situated at the six of this MiG-21. He’s well within range…maybe 1000’ or less. He’s at low angle off, with his closure under control, and in plane with the MiG. He’s got a good radar lock on so his gunsight has accurate ranging. But the pilot has two little problems. One is that the pipper is behind the MiG as the pilot chases the bandit in a descending turn. The other is that the pilot is pulling the trigger. He’s got a full load of 20mm tracer, and, as you watch the film, you see the pilot spewing those beautiful cannon shells out into nowhere as he tries to work the pipper up to the MiG.

BRAAAP! BRAAAP! The tracers continue to fall just behind his target as the F-4 pilot moves the pipper ever so closer to the MiG. Finally the pipper is there! Smack dead center on the fuselage of the bandit….just as the Gatling Gun runs dry. Oh, the heartbreak!

Well, no doubt emotions run high in combat, but this day, our F-4 pilot could have used a bit more discipline. His Silver Star was there for the taking, but he blew the opportunity. Was it impatience or lack of skill? We’ll never know. In this article, I’m going to talk about the latter…the ‘skill’ part. The gun is not magic, nor is it an ‘I wish you were dead!’ weapon system. It may well be the most difficult of all air to air weapons systems to use, and its successful use is seldom a matter of luck. Skill in aerial gunnery is based on two factors…a solid foundation in the academics of the subject, and the opportunity to train realistically. Fortunately for us simmers, most of our simulations offer a realistic representation of a gun weapon system…so we can practice as much as we want. It’s the academic part that has been missing. Few manuals explain the gun system or offer tips on how to use it. That’s what this article is going to do. Explain the gun system, and then pass along a few pointers on how to employ it.

Here’s the overview. The available literature on gunsights and their use is fairly limited. To help make up for that, I’m going to make this article an in depth review of the subject. Because of its length, the article will be in three parts. Use this overview to jump to the parts that you are interested in.

Overview

Part One - Basic Theory.

Terminology definitions.

Gun line concept.

Harmonization.

Bullet density.

Lead angle problem.

- Lead for target motion.

- Gravity drop.

Part Two - Gunsight Types.

Fixed Sight.

Lead Computing Optical Sight Systems (LCOSS).

- Disturbed reticle – Pipper and Funnel.

- Director Systems.

Part Three - Attack Types and Techniques.

Tracking.

- Low aspect.

- High Aspect.

Non-Tracking (Snapshot).

Basic Theory

I know you all want to jump right into the part where we gun the bandit’s brains out, but, sadly, we’ll have to set that part aside for a time. The simple fact is that the more you understand gun employment theory, the better you are going to be at it. Sounds about right, you say. And it is…but this understanding comes at a price. And that price is your willingness to put a little study time into the various principles involved. My role in all of this is to take this academic mumbo-jumbo and make it as digestible as possible…and make it relevant to our sims at the same time.

We’ll start off with some definitions. Most of these are terms that you may have run across at one time or another. The definitions that I’m going to use are intended to get the idea across without getting too deep into rocket science. Gun employment theory can get real complex, real fast…I don’t want to do that, so I’ll keep it as simple as I can.

Definitions

Machine Gun versus Cannon. As far as fighter aircraft go, these terms are roughly related to the caliber of the gun. Anything up to .50 caliber is a machine gun…anything over that is a cannon.

Caliber. The caliber of a gun is the size of the round as measured by its diameter. The units may be inches or millimeters. A .50 caliber is about one half inch in diameter. A 20mm is about one inch in diameter. A 37mm round is about one and one half inches in diameter. The following figures show the relative sizes.

But diameter is only half the picture. As diameter increases, so does projectile length…and, consequently, projectile weight. The next figure makes this clear.

Kill mechanism. Projectile types include ball, armor piercing, incendiary, high explosive, and combinations of these.

Ball - Typical rifle round, not used in modern fighters. More suited for WW1 and early WW2.

Armor piercing - The round has a hardened steel core for penetration of aircraft structures.

Incendiary - The round contains a chemical that ignites upon impact. Good for setting fuel and hydraulics on fire.

High explosive - Similar to the incendiary round, except the chemical has more destructive power.

Combination – The above round types can be combined…HEI (high explosive, incendiary), API (armor piercing, incendiary) for extra hitting power.

Rate of fire. Also known as cyclic rate. This is the number of rounds fired in a given amount of time, usually rounds per minute (rpm). May be expressed for a single gun or multiples. Some modern guns, such as the Gatling 20mm, may have cockpit selectable rates of fire. For example, the F/A-18E pilot can select a 4000 or 6000 rpm setting. The A-10 pilot can select either 2000 or 4000 rpm. Korean War and earlier gun types did not offer this feature.

In Figure 4 and 7, the colored horizontal lines represent values for typical WW2 guns. You can compare these lines to the modern day guns shown in the figures.

Muzzle velocity. The speed that the round leaves the barrel. Usually expressed in feet per second (fps) or meters per second (mps). Most modern gun types have muzzle velocities around 3000 fps. After leaving the barrel, the projectile will decelerate as a function of its unique ballistic characteristics. The modern US 20mm round has improvements that have greatly increased its ability to retain a high velocity. Other rounds, such as the Soviet 37mm in the MiG-15, have a low muzzle velocity to begin with that is further degraded due to high drag during its time of flight.

Time of flight (TOF). The time it takes the round after leaving the barrel to reach the target. Usually measured in seconds.

Dispersion. A target shooter will fire his rifle a number of times to establish a ‘group.’ The smaller the group, the more accurate the shooter is. A modern aircraft gun has a similar characteristic. Technicians will fire the gun at a target and then count the projectile impacts and measure their pattern from the center aim point. Typically, this calculation will be expressed as a percentage of rounds fired within a certain area, usually a circle with the aim point at its center, and is called the gun dispersion. A typical modern gun dispersion results in about 80% of the rounds being grouped in a five foot diameter circle at a range of 1000 feet.

 

Weight of fire. A concept used to describe hitting power. More often used in Korean War and earlier gun types. Literally expressed as ‘x’ amount of weight in a given period of time. A good example is the Spitfire with its eight .303 caliber guns. Even though the gun had a small caliber, it had a relatively high rate of fire, and when all eight fired in unison, the amount of lead being thrown was considerable. Because of the lethality of the modern aircraft cannon round, this term is seldom used anymore.

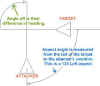
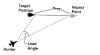
Angle off. This refers to the relative headings of the fighter and its target. Angle off is simply the difference in the direction the two aircraft are pointing. If they are pointing in the same direction, the angle off is zero…if they are approaching head on, then the angle off is 180 degrees. Angle off is a measurement of heading.

Aspect angle. This term is a measurement of position. The heading of the attacker relative to the target is irrelevant. Aspect angle refers to the attacker and is measured using the target as the reference. This measurement originates at the target’s six o’clock. This is the zero aspect position. The twelve o’clock position off the target’s nose is the 180 degree aspect position. From the six o’clock position to the twelve o’clock, aspect angles are referred to as either ‘right’ or ‘left.’ This is in reference to what side of the target you as the attacker are looking at. If you are looking at the target from its 3 o’clock position, you have a 90 Right aspect. And if you are looking at the target from its 7:30 position, you have a 45 Left aspect. Remember, your heading is not included in this term. Aspect angle is only a way of defining your position relative to the target.

Note: Aspect and angle off tend to be used in the same manner when we talk about gun attacks. This is a unique situation and occurs because we are usually thinking of the attacker being pointed at the target. When the attacker has his nose on the target, then his angle off and aspect are basically the same. In this discussion, I’ll use the term ‘angle off’ with this in mind.

Target apparent size. We all recognize the significance of target size. Big targets are easier to hit than small ones!! Target apparent size refers to a single target and how it looks from various angles. If we shoot at a target from its dead six, we have a much smaller target size than if we were to fire at it from directly above. Planform is a term that refers to target apparent size. Planform is greatest when looking down on the target. The greater the planform, the better chance of hitting the target. Planform and aspect angle have much in common since they both refer to how the target appears from the shooter’s perspective.

Ballistics computer. This device takes into account range, closure, and altitude values to arrive at a TOF computation. The TOF value is used to then compute a gravity drop correction.

Gunsight computer. I’ll use this term in the broad sense to refer to the device that takes into account target position (range, aspect, angle off, closure, rate of turn, etc) to compute the lead for target motion value.

Line of sight rate (LOS). The LOS is the speed that the target is crossing your gun line. This value is zero in a head on or tail aspect, and is maximum when the target is at 90 degrees angle off.

The Gun Line Concept

If you were to look through the barrel of the gun out to infinity, you would be looking along the gun line. The gun line establishes the initial vector of the round as it leaves the barrel (also known as the line of departure, the LOD). The gun line is an important part of the process of matching up the gun sight to the gun in an aircraft. It is the basis upon which all other calculations are made. If an aircraft has multiple guns, therefore it has multiple gun lines.

In our modern aircraft HUDs, the gun line is often represented by a small cross. This cross is ‘fixed’, meaning it doesn’t move. You can think of it as being similar to the sight on the end of a rifle. It is one way of visualizing where the gun is aimed.

The Sight Line Concept

The sight line is similar to the gun line. It too is a line from the eye to infinity, but this time, we are talking about the pilot’s eye as seen from the cockpit. Since few guns are co-located in the cockpit, there is a difference in the physical location of the gun line and the sight line. The following figure illustrates this difference.

Gravity Drop

Once the round leaves the barrel, it becomes a falling object subject to the laws of gravity. A round will drop approximately 16 feet in its first second of flight. The next figure will give you an appreciation of this factor. In this figure, notice that the pipper in the reticle is below the gun cross. The aircraft is in wings level flight at one G. The pipper position represents the gravity drop of the round over the range that the sight is computing for. As you can see, gravity drop is not an insignificant value as TOF increases.

Harmonization

In discussing harmonization, we will use the concepts of gun line, sight line, and gravity drop. Harmonization is the process of lining up the gun line so that it intersects the sight line at some point in front of the aircraft. The TOF for the round to cover that distance will be computed and used to calculate a gravity drop value. That value will be added to the gun line. Then the gun(s) will be adjusted so that the resulting projectile path (including gravity drop) will intersect the sight line.

In older fighters that had guns installed in the wings and nose, harmonization was much more of a factor to be considered. The basic idea is to adjust the guns so that all the gun lines converge at a predetermined distance. Why, you ask? Some might think it would be better to have the guns adjusted to spread out the gun lines...that way the pilot might have a better chance of hitting something. Now, there is a smidgen of logic to that idea, but only a smidgen. The better idea is to have the gun lines come together. That way the pilot has a highly concentrated area of fire that will deliver a killing blow to whatever it hits. Certainly, that area may be relatively small, but the issue is not the size of the projectile impact area. Instead, the issue is accuracy in aiming. We’ll get to that eventually. For now, we just want to establish the idea that harmonization is the process of converging gun lines so that they intersect the sight line at a predetermined distance.

During WW2, harmonization was a hot topic among pilots. The debate raged back and forth over what range the guns should be harmonized at. Some liked a short range…short being in around 300 feet. Others wanted the range a bit further out…as much as 1000 feet. In many fighter units, the matter was left up to individual preference.

Projectile Density

In simple terms, projectile density refers to how many bullets we can expect to have in a given amount of space at a particular point in front of our aircraft. We all immediately recognize that the denser the bullet pattern, the greater chance we have of hitting our target.

We have all seen the WW1 movies of the Red Baron blasting away at his opponent. Rat-tat-tat-tat! One, maybe two small caliber machine guns. A moderate rate of fire for the time. But nothing like the modern guns of today’s fighters. Today, the common perception is that a fighter’s gun fire is like a red hot laser beam. Well, not quite!!

Let’s try to interject a reality check to the matter of projectile density. What you want to take away from this part of the discussion is the understanding of how angle off and aspect angle affect your chances of hitting your target.

We’ve all heard it before. "Man!! That Gatling spits out 100 rounds a second! Nothing can escape that kind of firepower." If only it were so. Too often, the typical person visualizes those 100 rounds all in the same spot. Not true. A little math will make this clear.

Let’s fire a one second burst from our M61. 100 rounds, just for argument’s sake. Now let’s picture what the bullet stream looks like. For starters, it’s 3000 feet long…remember muzzle velocity. As the last round is coming out of the barrel, the first round is one half mile away! Spread those rounds out over that distance, and we end up with one round every 30 feet. Then we have to remember dispersion. The bullet stream is not a ‘frozen rope.’ Instead, it is a cone that is about 15-20 feet in diameter at 3000’.

One round every 30 feet! Not exactly the blizzard of fire that some might think. And then those rounds get spread around due to dispersion. That doesn’t help things much. But there is one more parameter that we need to look at, and that is the relationship of the target’s flight path to our bullet stream.

If we are at the target’s dead six and are shooting at it, then many of the rounds have a chance of getting a hit. This is because the target remains in the general area of the bullet stream during the entire burst length. But what happens if the target is crossing the bullet stream? Whoa!! Our neat little picture of instant target obliteration takes a big hit (no pun intended!). Let’s use a little math again to make the point. Let’s have the target cross the bullet stream at 90 degrees. We’ll say the target is doing 500 knots…that will give it a speed of about 850 feet per second. The target is a typical modern fighter with a length of about 60 feet. How long does it take the target to cross the bullet stream? About one tenth of a second! We remember our rate of fire was 6000rpm or about 100 rounds per second…so, in 1/10 of a second, only about 10 rounds have a chance of hitting the target. Now, we throw dispersion into the equation and our chances of hitting the target become even less.

It is very important to visualize the bullet stream as three dimensional. In the next screenshot, the bullet stream is represented by a funnel display. The funnel extends below the gun line and appears to run through the target. Because of this fact, this may look like a valid aiming solution. But it is not. In fact the rounds that are at target range are in front of the target…this aiming solution has too much lead.

Figure 16 is a drawing of what the situation in Figure 15 would look like from a side view. This drawing when combined with the screenshot gives you the complete picture…a three dimensional visualization that makes the concept of the bullet stream much more meaningful.

In seeing the bullet stream in this manner, significance of target angle off and apparent size becomes all too clear. The faster the target moves through the bullet stream, the less chance it has to be hit. If we as the shooter can do something to keep the target in the bullet stream longer, then we increase our chances of success. This is an aiming problem, and since this article is ultimately about aiming the gun, we’ll now move on to looking at that problem. We’ll call that problem ‘the lead angle solution.’

The Lead Angle Problem

There are two variables to solve for when we look at the lead angle problem. First, let’s identify that problem. We are in a gun platform that is moving. We are trying to hit a target that is also moving. We intend to shoot rounds at the target…this will take a certain amount of time (TOF) and this in turn will result in some gravity drop.

The problem then is to fire our gun having taken into consideration two things…lead for target motion, and gravity drop. The next figure is a common illustration of the lead angle problem found in many sim manuals. Both the attacker and target are flying straight. The situation is similar to a skeet shooting problem. We’ll use this figure to discuss the problems in computing lead for target motion and gravity drop.

Computing the lead angle. In a gun attack, the firing geometry can range from a pure tail chase to a head on set up. Clearly, the lead for target motion is greatest when the target angle off is 90 degrees and is essentially zero when the angle off is zero or 180 degrees. The gunsight computer must solve for this value, and the first question that always came to my mind was ‘how does the computer know where and what the target is doing?’ Believe me…when it comes to gunsight computations, that is the $64,000 question!!

Our illustration shows a target that is not turning. Throw in a turning target, and the problem becomes very difficult to solve. In fact, it has only been in recent years that radar technology and computer improvements have been able to come close to an accurate answer. Prior to these new systems, gunsight computers used a number of assumptions about both the attacker’s and target’s flight behavior to arrive at a solution. As you might expect, life seldom matched these assumptions, and the resulting lead angle solutions were only approximate at best. Some of these assumptions included the following: the two aircraft were co-speed…the aircraft true air speed was a certain value…the range was fixed…the altitude was a constant…if the target was turning, it was turning at the same rate as the attacker. It was a lucky day for the attacking pilot when these assumptions matched the actual firing situation. More often than not, this was not the case, and the pilot had to fall back upon prior experience to make up for errors in his sight system.

Computing gravity drop. We have already shown that the gravity drop value is a function of TOF. Many of the assumptions mentioned above also have a negative impact on the gravity drop calculation. Incorrect closure, range, and altitude values all result in errors…while the gravity drop part of the total lead angle is usually much smaller than the lead angle part, the value is still significant to the overall gunnery solution.

Putting it all together. The next figure shows a hypothetical (and simplistic) view of the lead angle solution. In Part Two, we will go into each gunsight type in detail and explain how each type either does or does not replicate this view.

Click here to go to top of this page.